El título de esta reflexión son palabras expresadas por Ubiratan D’Ambrosio en el marco del Primer Congreso Internacional de la Asociación Nacional de Profesores de Matemática en Toluca, México.
Su conferencia trataba del impacto de las calculadoras de bolsillo en la educación científica, sin embargo este visionario de la Educación Matemática hacía un recuento histórico de cómo las ideas nuevas siempre han tenido un camino escabroso hacia su aceptación antes de que el tiempo se encargue de incorporarlas.

Estas palabras fueron dichas en febrero de 1978 pero siguen teniendo vigencia en el contexto educativo actual. Voy a mencionar lo que considero un ejemplo.
Una disputa más…
En 2012, Costa Rica dio un gran salto cualitativo al modernizar su Currículo de Matemática para la educación primaria y secundaria. Este incorporó resultados de investigaciones y buenas prácticas de la Educación Matemática no solo en Costa Rica sino en el mundo; se afirmó entonces una perspectiva para la preparación escolar matemática que subrayó el desarrollo de una competencia matemática al servicio de la ciudadanía y capacidades superiores, e incorporó papeles relevantes para los contextos reales y las tecnologías, así como el cultivo de actitudes positivas hacia las matemáticas y su enseñanza. Se trataba de una nueva perspectiva educativa; sin embargo, estos cambios tan profundos generaron una reacción negativa en algunos sectores educativos. En esta ocasión sólo me referiré a la enseñanza de la Estadística y Probabilidad, un área central de los Programas de estudio de Matemática (MEP, 2012).
En parte debido a una débil formación disciplinaria y didáctica en Estadística y Probabilidad, algunos docentes de primaria y secundaria tuvieron una resistencia inicial a la enseñanza de estos contenidos (Alpízar et al., 2012; Alpízar, Chavarría y Oviedo, 2015; Chaves, 2007). Esta reacción, que se puede considerar natural, poco a poco ha ido cambiando. Especialmente porque a los estudiantes les entusiasma mucho trabajar con esta área. No obstante, queda mucho camino por recorrer y se debe fortalecer la preparación docente en esta área.
Siguen siendo preocupantes comentarios de algunos académicos de Universidades, cada vez menos afortunadamente, los cuales han manifestado que la formación estocástica tiene poca relevancia para los futuros profesionales; incluso estos han considerado que eran más importantes otros contenidos que no se incluyeron en el currículo actual (por ejemplo, funciones trigonométricas). En estos comentarios se exhibe una perspectiva curricular tradicional que enfatiza solo los contenidos y no aquella que proponen los programas de estudio actuales que sostiene el desarrollo de habilidades.
Pero, ¿por qué es importante el desarrollo del razonamiento probabilístico?
La disputa entre las ideas viejas y las nuevas históricamente han estado presentes; una de ellas precisamente es la que se da entre el determinismo y la aleatoriedad en las teorías físicas. La interpretación probabilística realizada por Werner Heisenberg, con base en lo que se llamó “Principio de incertidumbre”, generó un rechazo entre los que defendían el determinismo en la Física.
La idea de un electrón en movimiento acompañado siempre por una serie de ondas, hace que desaparezcan las órbitas deterministas de los primeros modelos atómicos y se sustituyan por las expresiones de probabilidad o funciones de onda ideadas por Erwin Schrödinger. Esto originó el surgimiento de la Mecánica Cuántica que tenía un elemento que no consideraba la Mecánica clásica: el azar.
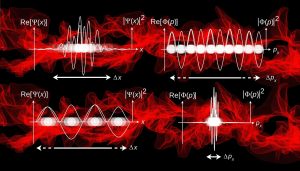
El ejemplo anterior, ilustra que la teoría probabilística ha impactado distintas ideas científicas, y esto ha repercutido en los currículos de matemáticas de varios países, en donde se introducen contenidos de probabilidad desde edades tempranas (Por ejemplo: Australia, Australian Curriculum, Assessment and Reporting Authority, 2013; España, Ministerio de Educación, Cultura y Deporte, MECD, 2014 y Estados Unidos de América, National Council of Teachers of Mathematics, 1989; 2000). En países como China, la inclusión de contenidos de probabilidad se retrasó respecto a los planes de estudio europeos y estadounidenses, y no ha sido hasta el 2001 en los Estándares del Currículo de Matemáticas para la Educación Obligatoria que se incluyó como una rama de contenido en el currículo obligatorio (Gong y He, 2017).
¿Qué decir de la alfabetización estadística?
Por otro lado, creo que sería reiterativo decir, en un contexto de Pandemia, lo importante que es para la persona común poder entender el flujo de información estadística que le llega de los distintos medios de comunicación; pero además, el análisis de datos se ha convertido en una herramienta utilizada por muchos campos profesionales, buscando la mejora de la productividad y calidad en el desarrollo industrial y comercial; sobre todo en la toma de decisiones a partir de datos estadísticos, para lo cual se requieren algunas habilidades, las cuales Batanero (2002) enmarca con los términos de “alfabetización estadística”.

Estas corrientes curriculares han influenciado también al Programa para la Evaluación Internacional de los Estudiantes (PISA) de la Organización para la Cooperación y el Desarrollo Económicos (OCDE); y este a su vez, ha influido en la toma de decisiones en política educativa no solo de los países participantes sino también en los que tienen la intención de hacerlo en algún momento. Considerando las recomendaciones relativas a los currículos escolares, donde sugieren unánimemente la incorporación de la estadística y la probabilidad, en el marco teórico PISA 2003 (OCDE, 2003) dan paso a la cuarta idea principal: la incertidumbre. La cual sería tratada desde una perspectiva matemática y científica, asociando dos temas, los datos y el azar; son objeto de estudio matemático por parte de la estadística y de la probabilidad, respectivamente.
Por su parte, fieles a las corrientes educativas modernas, el currículo actual de Costa Rica le dio gran relevancia al área Estadística y Probabilidad, con un enfoque más cercano a la naturaleza de la disciplina, cuyos conocimientos y expectativas de aprendizaje se organizan de manera integrada desde el primer año de educación primaria hasta el último de educación secundaria. Este es un hecho notable, puesto que en programas de estudio anteriores había pocos contenidos de Estadística en primaria; y menor cantidad en secundaria, donde aparecen en forma aislada (Chaves, 2007). Además, en educación secundaria no aparecían contenidos de probabilidad, por lo que los pocos temas que estaban en educación primaria habían sido “invisibilizados” por los docentes, priorizando otros contenidos que sí tenían continuidad en el siguiente nivel educativo.
¿Qué ha ocurrido hasta ahora?
Desde hace muchos años investigaciones nacionales e internacionales serias sostienen que esta área matemática es fundamental para la formación integral del ciudadano actual. Por eso en el Currículo de Matemática costarricense esta constituye un ente catalizador de las demás áreas del currículo, apoyando en particular la resolución de problemas en contextos reales.

Desafortunadamente, en los últimos años en Costa Rica, Estadística y Probabilidad se vieron afectadas en casi todos los niveles educativos: “El desarrollo de las habilidades matemáticas más afectadas durante 2018 y 2020 fueron las relacionadas con el área de estadística y probabilidad” (PEN, 2021, p.109). Mucho se debió al “apagón educativo”.
La implementación de la enseñanza de Estadística y Probabilidad requiere fortalecer la preparación docente (inicial y en servicio) en esta área y que el MEP continúeL apoyando su desarrollo en congruencia con el currículo nacional.
Reflexión final
En un escenario en que el ciudadano está “bombardeado” por un gran volumen de datos estadísticos proveniente de diferentes fuentes (diarios, revistas, noticieros, redes sociales, etc.), es imperativa una alfabetización estadística en la población. Solo así se podría preparar a la población para la toma de decisiones colectivas y personales con base en la interpretación de la información y el pensamiento crítico (Schiller y Engel, 2016). Y no solo Estadística en sí misma: los conocimientos probabilísticos deben formar parte de los objetivos de alfabetización matemática para los ciudadanos (Jones, Langrall y Mooney, 2007; Nilsson y Li, 2015). Es lo que se llamaría una “alfabetización estocástica”.
Ubiratán D’Ambrosio decía en su discurso: “El rechazo tal vez es la fuerza más activa contra los cambios y contra la dinámica que debe prevalecer necesariamente en el proceso educativo”. Y por eso la resistencia al cambio o la incorporación de nuevas ideas puede considerarse una reacción natural en el ser humano, pero no puede permanecer por mucho tiempo y los profesionales en educación deben asumir el reto.
Referencias
Alpízar, M., Barrantes, J., Bolaños, H., Céspedes, M., Delgado, E., Freer, D., Padilla, E., y Víquez, M. (2012). Aspectos relevantes sobre la formación docente en I y II ciclos en los temas Probabilidad y Estadística. EDUCARE, 16(2), 113-129.
Alpízar, M., Chavarría, L. y Oviedo, K. (2015). Percepción de un grupo de docentes de I y II ciclo de educación general básica de escuelas públicas de Heredia sobre los temas de estadística y probabilidad. Actualidades Investigativas en Educación, 15(1), 1-23. DOI: dx.doi.org/10.15517/aie.v15i1.17728
Australian Curriculum, Assessment and Reporting Authority (ACARA) (2013). The Australian curriculum: Mathematics. Sidney, NSW: Author.
Batanero, C. (2002). Los retos de la cultura estadística. Yupana, 1(04), 27- 37.
Chaves, E. (2007). Inconsistencia entre los programas de estudio y la realidad de aula en la enseñanza de la estadística de secundaria. Actualidades Investigativas en Educación, 7(3), 1-35.
Chaves, E. (2020). Crisis del sistema educativo costarricense a consecuencia de las huelgas y la Pandemia: efectos en la alfabetización estadística. Cuadernos de Investigación y Formación en Educación Matemática, 19, 54–72.
D’Ambrosio, U. (1978). El impacto de las calculadoras de bolsillo en la educación científica y en particular en la enseñanza de las Matemáticas. En: Primer Congreso Internacional de la Asociación Nacional de Profesores de Matemática, Toluca, México (pp.9-18).
Gong, Z. y He, S. (2017). Developmental stages and important periods of probability cognition in 6 to 14 year-old students. AIEM, 11, 47 – 68
Jones, G., Langrall, C., y Mooney, E. (2007). Research in probability: responding to classroom realities. En F. Lester (Ed.), Second handbook of research on mathematics teaching and learning (vol. 2, pp. 909-955). Greenwich, CT: Information Age Publishing y NCTM.
Ministerio de Educación, Cultura y Deporte, MECD (2014). Real Decreto 1105/2014, de 26 de diciembre, por el que se establece el currículo básico de la Educación Secundaria Obligatoria y del Bachillerato. Madrid: Autor.
Ministerio de Educación Pública (MEP). (2012). Programas de Estudio de Matemáticas. I, II Y III Ciclos de la Educación General Básica y Ciclo Diversificado. San José: Autor.
National Council of Teachers of Mathematics (NCTM) (1989). Curriculum and evaluation standards for school mathematics. Reston, VA: The Council.
National Council of Teachers of Mathematics (NCTM) (2000). Principles and standards for school mathematics. Reston, VA: The Council.
Nilsson, P., y Li, J. (2015). Teaching and learning of probability. En S. J. Cho (Ed.). The Proceedings of the 12th International Congress on Mathematical Education: Intellectual and Attitudinal Challenges (pp. 437-442). New York: Springer.
OECD. (2003). The PISA 2003 Assessment Framework: Mathematicas, Reading, Science and Problem Solving Knowledge and Skills. Paris: PISA, OECD Publishing.
PEN. (2017). Octavo Informe del Estado de la Educación. San José: Programa Estado de la Nación.
Poveda, R. y Manning, G. (2021a). Las repercusiones de la huelga del 2018 y la Covid-19 en la aplicación de los Programas de Estudio de Matemáticas. Ponencia preparada para el Octavo Informe Estado de la Educación. San José: PEN, Conare.
Ruiz, A. (2020). Reforma Matemática en tiempos de crisis nacional: fortalezas, debilidades, amenazas, oportunidades. Cuadernos de Investigación y Formación en Educación Matemática, 19, 9–53.
Schiller & Engel (2016). Civic statistics and the preparation of future secondary school mathematics teachers. In: J. Engel (Ed.), Promoting understanding of statistics about society.Proceedings of the Roundtable Conference of the International Association of Statistics Education (IASE), July 2016, Berlin, Germany.



















