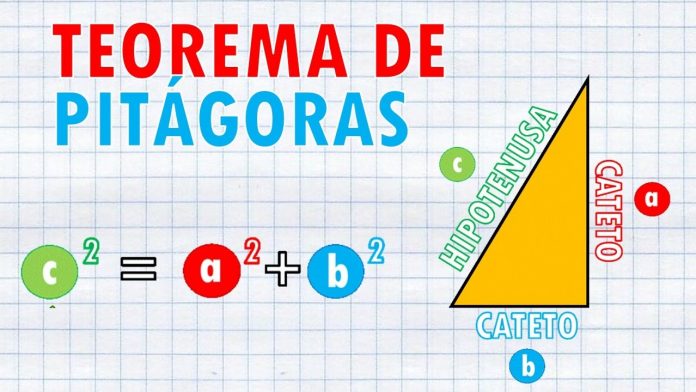
Sin ninguna duda, uno de los resultados más sobresalientes que existen en la geometría euclídea es el famoso Teorema de Pitágoras, que permite establecer una relación entre los catetos y la hipotenusa de los triángulos rectángulos. Este teorema es conocido desde las civilizaciones antiguas como la mesopotámica o la egipcia, quienes utilizaban este resultado para resolver problemas relacionados con este tipo de triángulos (Gómez, 2017). El enunciado formal de este teorema es:
En cualquier triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
De este resultado existen muchas demostraciones formales. Algunos matemáticos afirman conocer mas de mil maneras diferentes de justificar el resultado (Gómez, 2017). En este trabajo, se busca analizar el impacto que tiene este teorema en la educación secundaria costarricense, en la enseñanza de temas posteriores de geometría euclídea, e inclusive en otras áreas de la matemática. A continuación, se van a enunciar varias temáticas del Plan de Estudios de Matemáticas del MEP (2012), en las cuales es fundamental el conocimiento del Teorema de Pitágoras:
Distancia entre dos puntos ubicados en el plano cartesiano
Un conocimiento que se debe explicar a los estudiantes es la fórmula de distancia entre dos puntos del plano cartesiano. Para esto, se debe utilizar la fórmula que indica que si se tienen los puntos P(x,y) y Q(a,b), entonces se cumple que:
d(P,Q)=(x-a)^2+(y-b)^2
La cual, se deduce a partir de considerar las coordenadas (x-a) y (y-b) como catetos de un triángulo rectángulo en el plano cartesiano, es decir, acá tenemos una aplicación del teorema de Pitágoras a la enseñanza de la geometría analítica.
Resolución de problemas de triángulos con ángulos de elevación y depresión
En el área de la trigonometría, las razones trigonométricas son de utilidad para encontrar lados o ángulos de los triángulos rectángulos, sin embargo, siempre se da como alternativa que cuando el estudiante ya posee las medidas de dos lados, pueda hallar la medida del tercer lado utilizando el teorema de Pitágoras, es decir, lo podemos aplicar en la resolución de problemas de ángulos de elevación y depresión.
Pirámide recta
En estereometría cuando se tiene una pirámide de base rectangular, se puede establecer una equivalencia entre la apotema, la medida del lado de la base y la altura, esto a partir del teorema de Pitágoras aplicado en el triángulo naranja, la cuál se describe a continuación:
(l/2)^2+h^2=Ap^2
Esto puede ser útil para el cálculo de áreas laterales, basales y volúmenes de la pirámide.
Longitud de segmentos que se forman al intersecar una circunferencia y su recta tangente en un punto
Cuando se tienen problemas relacionados con una circunferencia, la recta tangente y un punto que pertenece a la tangente, se puede formular un triángulo rectángulo (tal y como se aprecia en la figura) que permite calcular medidas asociadas utilizando el teorema de Pitágoras, como el radio de la circunferencia, la distancia al punto de tangencia o la distancia al centro.
Cortes con planos realizados a las esferas
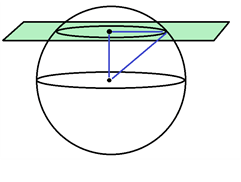Cuando se plantean problemas relacionados con los cortes que genera la intersección de una esfera y un plano en el espacio tridimensional, se forma un triángulo rectángulo (ver figura) donde el radio de la esfera coincide con la hipotenusa de un triángulo rectángulo, y los catetos son la distancia del centro al corte y el radio del sector circular resultante al cortar la esfera. Es así como para calcular estas distancias podemos aplicar el teorema de Pitágoras.
Polígonos regulares
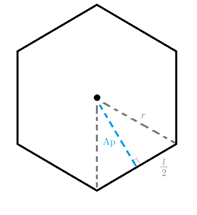En la temática de polígonos regulares, existen tres datos fundamentales para calcular áreas y perímetros, que son las medidas de los lados, la apotema y el radio del polígono. Por la definición y relación de estos tres componentes, se deduce la siguiente fórmula:
(l/2)^2+Ap^2=r^2
Lo cual se justifica en que estos tres componentes conforman un triángulo rectángulo como se aprecia en la figura, y por tanto, es una aplicación directa del teorema de Pitágoras.
Cono circular recto
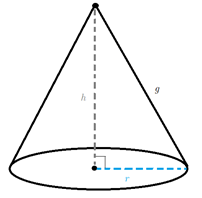De manera similar al caso de las pirámides rectas, a la hora de realizar un corte interno a un cono circular recto, se obtiene una relación entre la generatriz, el radio y la altura, pues se forma un triángulo rectángulo, y al aplicar el teorema de Pitágoras se obtiene que:
r^2+h^2=g^2
Tal y como se ha podido apreciar, el teorema de Pitágoras no debe ser visto como una temática cualquiera a nivel de secundaria, pues es un contenido fundamental para el futuro rendimiento de los estudiantes en temáticas de la misma geometría euclídea, de la trigonometría, de la geometría analítica y la estereometría.
Por todo esto, los futuros docentes de matemáticas, debemos desarrollar esta temática con mucho empeño y dedicación en que los estudiantes adquieran un verdadero aprendizaje significativo, pues en caso de que no se desarrollen habilidades en esta temática, esto podría repercutir en que no se comprendan otras temáticas a futuro. Para cumplir con este objetivo debemos tratar de ser lo más creativos y propositivos de actividades didácticas en las que los estudiantes puedan comprender a cabalidad este tema.
Referencias Bibliográficas
Gómez, L. (2017). Matemática 9: Desarrollando habilidades. Editorial PIMAS. San José, Costa Rica
Ministerio de Educación Pública. (2012). Programas de estudios de matemáticas, I y II ciclo de la educación primaria, III Ciclo de la educación general básica y educación diversificada. San José, Costa Rica.
