En el universo geométrico vive una gran cantidad de objetos que, por diversas razones, son de gran interés. Algunos son simples como el punto, la recta, la circunferencia, los polígonos en general, etc. Otros son menos simples, como las secciones cónicas, diversos tipos de espirales, cardioides, rosas de diverso número de pétalos y más. Esto constriñéndonos solamente al plano.
Muchos de los objetos más complejos, por lo general, no son considerados en los planes de estudio de matemáticas en los niveles primario o secundario. Sin embargo, algunos pueden ser introducidos, al menos parcialmente, mediante actividades especiales en la clase, en el contexto del estudio de otras figuras.
Espiral logarítmica
A propósito del estudio de propiedades del triángulo rectángulo se puede introducir la espiral logarítmica. En esta sección se sigue a grandes rasgos el planteamiento de Kappraj (2015).
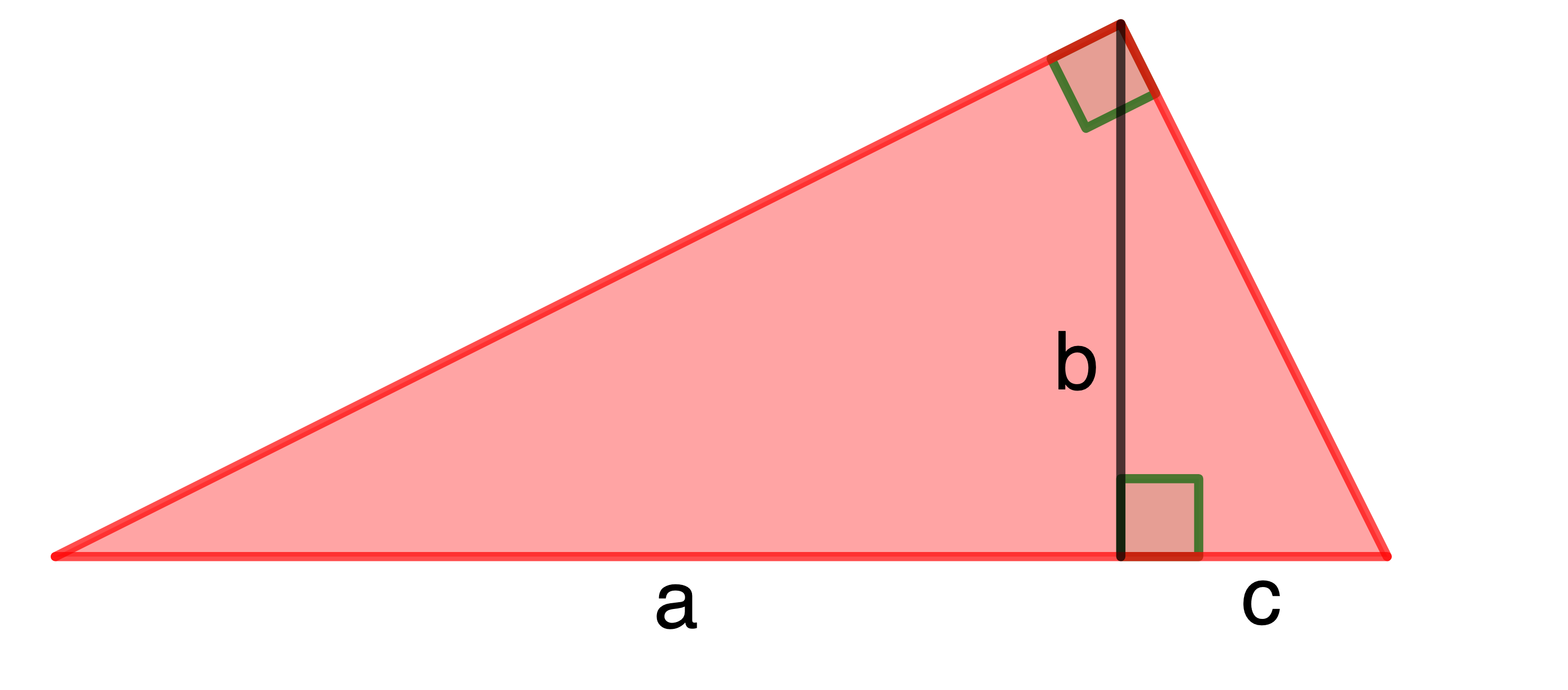
Recuerde que si se tiene un triángulo rectángulo y se traza la altura -de medida b- desde el ángulo recto, el punto en el que la altura corta la hipotenusa la divide en dos segmentos de medidas a y c y se tiene la propiedad ![]()
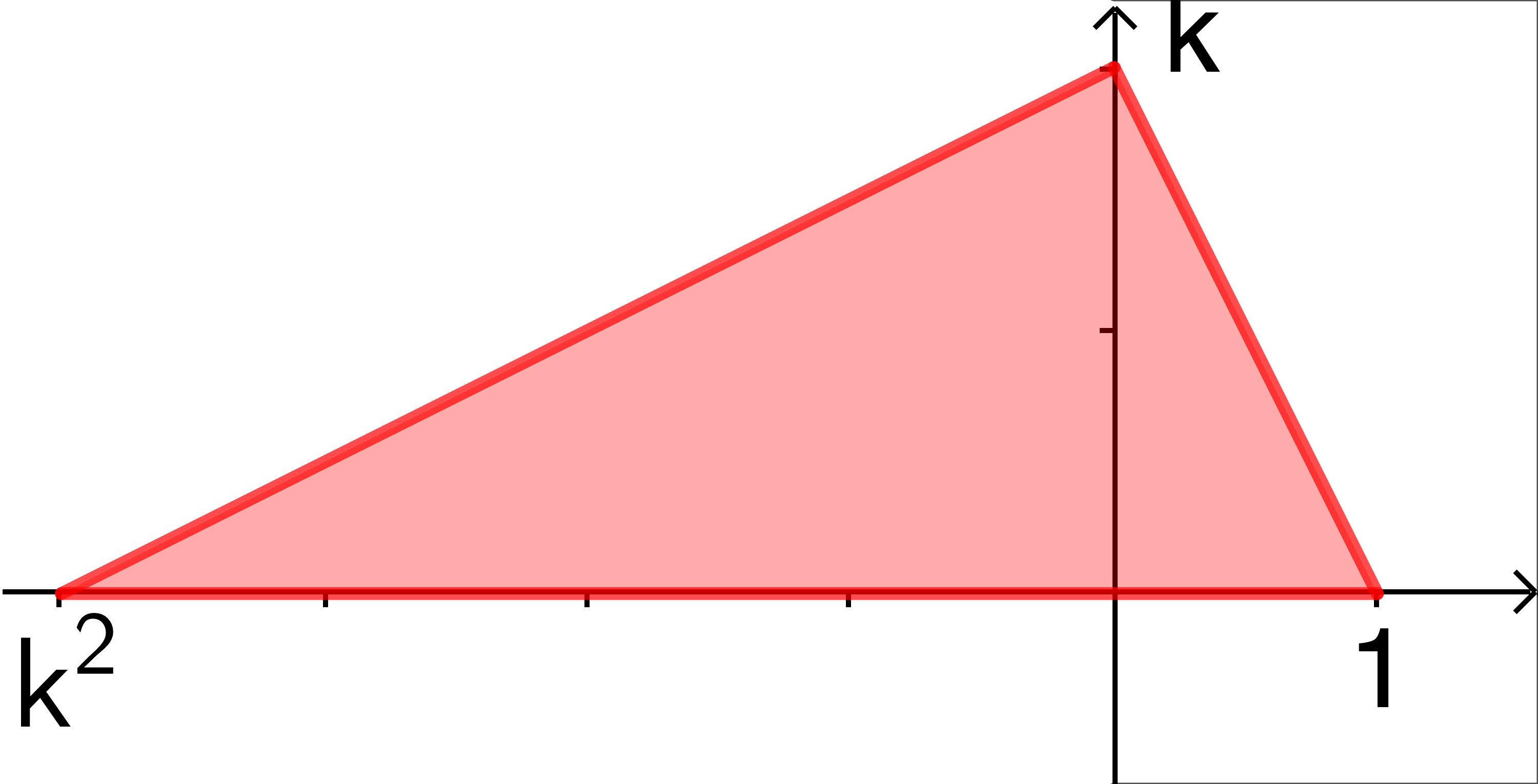
Considere un sistema de coordenadas cartesianas y construya un triángulo de base 1 -un vértice es (1,0)- y altura sobre la hipotenusa igual a k -otro vértice es el punto (0,k). Para ubicar el tercer vértice (-x,0), usamos el hecho de que ![]() tal como lo muestra la figura:
tal como lo muestra la figura:
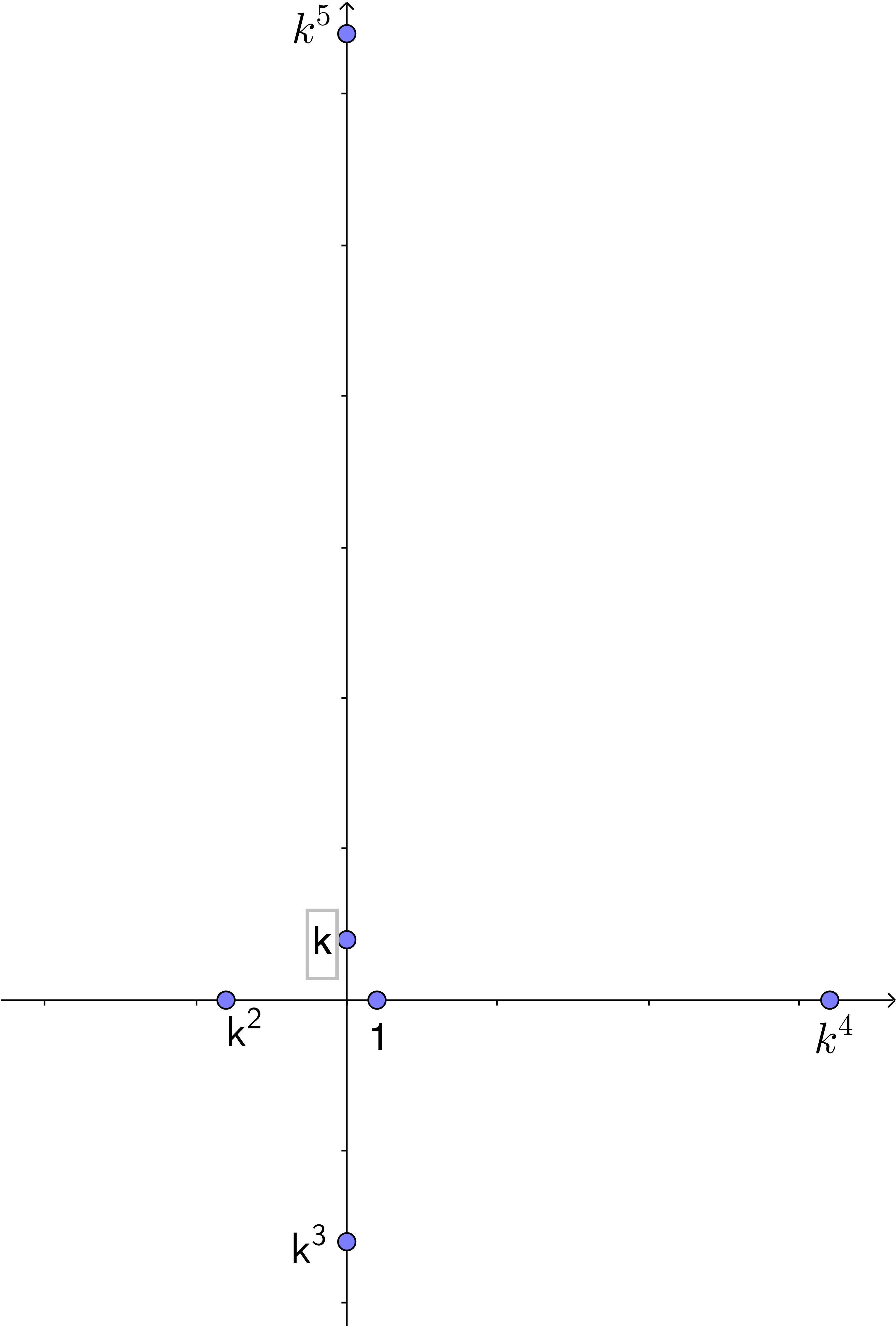
Luego ubicamos otro punto (0,x1) tal que ![]()
y así sucesivamente, se obtiene una sucesión de puntos como muestra la figura:
Todos estos puntos pertenecen a una espiral logarítmica.
Si consideramos los valores consecutivos de x, se obtiene una sucesión de números: ![]()
Llamemos a los puntos “vértices sobre una espiral logarítmica”. Si construimos la tabla siguiente, donde n corresponde al número de ángulos rectos que genera cada vértice y r es la distancia del vértice al origen del sistema de coordenadas se tiene:
Esta tabla corresponde a la función ![]()
aplicada a los números enteros no negativos de x. Si se lee la tabla de derecha a izquierda ella corresponde a la función ![]()
para las potencias enteras no negativas de 2 -por eso se llama espiral logarítmica-.
Construcción de la espiral
Los vértices que hemos encontrado previamente sirven como base para la construcción final. Cada par de vértices consecutivos se conecta con un arco de cierta circunferencia (un cuarto de circunferencia).
Existen recursos en internet donde se indica como construir una espiral logarítmica, siguiendo una serie de pasos -como una receta-; por ejemplo en https://www.youtube.com/watch?v=a5vQFDKX1XE. En la siguiente figura se representa una espiral logarítmica.
Conclusión
Se pueden ver las posibilidades didácticas de la introducción de esta figura en particular, permite, por ejemplo, integrar diversas habilidades geométricas y algebraicas, en el sentido que, por ejemplo, se les da en MEP (2012). Esta habilidades relacionan propiedades del triángulo rectángulo, proporciones y funciones exponencial y logarítmica. Se podría utilizar en diferentes niveles enfocando su estudio parcialmente según las habilidades que se quieran potenciar.
Referencias
Dibujo de la espiral logarítmica. (2020). https://www.youtube.com/watch?v=a5vQFDKX1XE
Kappraj, J. (2015). A participatory approach to Modern Geometry. New Jersey: World Scientific.
Ministerio de Educación Pública [MEP]. (2012). Programas de Estudio de Matemáticas. I, II y III Ciclos de la Educación General Básica y Ciclo Diversificado. San José, Costa Rica: autor.