La manera en que el Ministerio de Educación Pública (MEP) incluye el término generalización en los Programas de Estudio de Matemáticas, sucede en dos sentidos: generalización en matemáticas y generalización en el aprendizaje. Por lo cual, cabe aclarar que, en este escrito, sólo se considera lo concerniente al primer tipo, es decir a la generalización matemática: se pretende dar una breve descripción sobre la forma que toma este proceso en cada ciclo escolar.
En primer lugar, es necesario indicar que, dentro de los ya mencionados programas de estudio, la mayor parte de habilidades acordes con la generalización matemática pertenecen al área de Relaciones y Álgebra, y se trabajan mediante el estudio de patrones y relaciones, funciones y relaciones simbólicas (MEP, 2012, p. 22).
Por ejemplo, en primer grado, como parte de la malla curricular, se estudia el resultado de sumar o restar cantidades con el fin de identificar su acción sobre los valores numéricos dados y generalizar esta noción a través de términos como “agregar”, “combinar”, “sustraer”, “quitar”, etc.
Sin embargo, tal construcción es sólo una porción de lo necesario para desarrollar habilidades propias de la generalización matemática en distintos niveles cognitivos; es decir, se requiere de un abordaje gradual y continuo para aprehender eficazmente el conocimiento implicado.
De esta forma, en el área de Relaciones y Álgebra de Primer ciclo, predominan las habilidades orientadas al estudio de sucesiones y patrones en listas de números o figuras geométricas.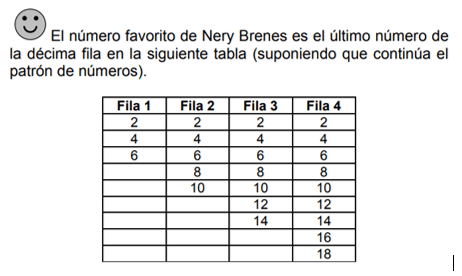
Problema para trabajar la habilidad de plantear y resolver problemas aplicando sucesiones y patrones en tercer año de primaria (MEP, 2012, p. 140)
Asimismo, para Segundo ciclo, MEP (2012) establece que “Relaciones y Álgebra prosigue con patrones numéricos, pero incluye representación de puntos en el plano cartesiano y de relaciones entre cantidades que varían y, algo muy importante, el razonamiento proporcional que conecta con las funciones” (p. 171).
Por otro lado, en Tercer ciclo, se profundiza en las relaciones que establecen las operaciones estudiadas en los ciclos anteriores, pero no su efecto sobre conjuntos específicos, ni los criterios que deben cumplir para establecer cierto tipo de relación; en su lugar, se pretende que el estudio de funciones sea un proceso más intuitivo que formal. No obstante, se requiere un mayor nivel de abstracción para operar variables y entender las propiedades vistas en aritmética en los ciclos anteriores, pero ahora usando representaciones literales.
Finalmente, en Ciclo diversificado se formaliza el concepto de función y sus distintas representaciones, y se trabajan los conceptos que en Tercer ciclo se vieron con menor detalle, por ejemplo, los conjuntos sobre los que actúan las funciones.
Es así como la generalización matemática forma parte del currículo nacional -desde primer grado hasta undécimo año-, en concordancia con la meta de “potenciar procesos de generalización y simbolización” (MEP, 2012, p. 22) en el área de Relaciones y Álgebra.
Referencias bibliográficas
Ministerio de Educación Pública. (2012). Programas de Estudios de Matemáticas. Costa Rica.