En la educación primaria se trabaja el área de Medidas y en la educación secundaria es transversal. El uso correcto de las unidades, de acuerdo al cálculo que se está realizando es fundamental. El simple hecho de entender el tipo de unidad de medida que resulta al final del cálculo que se está realizando, implica una familiarización más amena con la fórmula que lo modela.
Por ejemplo, usualmente hay una clara confusión con las fórmulas del área del círculo (π×r2) y del perímetro del círculo (2×π×r), donde puede suceder que sí se las hayan aprendido, sin embargo, confundan cuál es la del área y cuál es la del perímetro. Cabe destacar que dicha confusión se mantiene hasta secundaria e incluso a niveles universitarios.
Si el estudiantado comprendiera el porqué una es una unidad cuadrática y la otra es una unidad lineal, facilitaría el proceso de distinguirlas según su objetivo. Asimismo, las fórmulas de volumen, en algunos casos, se definen como el área de la base por la altura, es decir, una unidad cuadrática por una unidad lineal, donde debe dar como resultado una unidad cúbica.
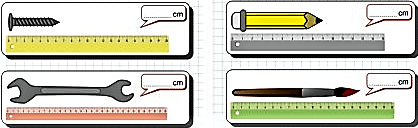
Para reforzar estos conceptos se propone un proceso progresivo de mediciones, pero siempre mencionando la unidad de medida que corresponde. Por ejemplo, determinar la longitud de cada una de las siguientes figuras.
Fuente: https://www.orientacionandujar.es/
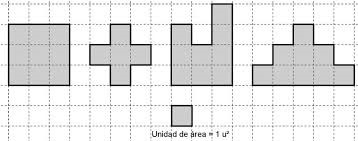
Posteriormente, en el cálculo de áreas, se puede utilizar la cuadrícula en vez de la regla, para inducir la idea de que se trabaja con dos dimensiones y de la misma forma que la anterior, resaltando la unidad de medida. Por ejemplo, calcular el área de las siguientes figuras, utilizando la técnica de conteo de cuadrados dentro de la figura.
Fuente: https://docplayer.es/
En donde, las respuestas esperadas, en orden, serían 9u2, 5u2, 9u2 y 9u2
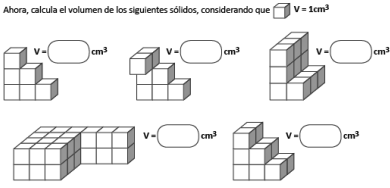
Asimismo, en el cálculo de volúmenes, se puede utilizar cubos, de forma tal que induzca que se trabaja con tres dimensiones, igual que los casos anteriores, resaltando la unidad de medida. Por ejemplo, determinar el volumen de los siguientes sólidos, utilizando la técnica del conteo de cubos dentro del sólido.
Fuente: https://www.pinterest.cl/
Donde, las respuestas esperadas son, en orden de izquierda a derecha, 6cm3, 7cm3, 12cm3, 30cm3 y 12cm3.
Ahora bien, ahora que conocen la unidad de medida según el objetivo de lo que se requiere calcular, es momento de relacionarlo con las fórmulas, cada longitud tiene una unidad lineal, así que por cada longitud que se vaya multiplicando en la fórmula se irá aumentando el grado de la unidad resultante.
Por ejemplo, el perímetro del cuadrado P=4×l o bien P=l+l+l+l, solo utiliza una longitud, así que la unidad es lineal. Ahora si queremos el área del cuadrado A=l2 o bien A=l×l, la longitud del lado se utiliza multiplicándose dos veces, entonces la unidad quedaría cuadrática. Finalmente, si quisiéramos calcular el volumen de un cubo, V=l3, o bien, V=l×l×l donde la longitud del lado se utiliza multiplicándose tres veces, es decir, la unidad queda cúbica. De esta forma se podrían dar varios ejemplos más con la misma idea de enfatizar en el grado de la unidad de medida.
Por último, a modo evaluativo, podría darse al estudiantado una serie de objetos para que los clasifique según el tipo de unidad de medida que tendrían, según lo que se le quiera calcular a dichos objetos, por ejemplo, subraye los que corresponde a longitudes, encierre en un cuadrado los que corresponden áreas y coloree los que corresponden a volúmenes.