Para la educación primaria costarricense (niños entre 6 y 12 años) se puede entender el pensamiento geométrico como la capacidad de la persona estudiante para visualizar en dos y tres dimensiones objetos geométricos, de manera que pueda clasificarlos, utilizarlos y emplear sus propiedades, tanto en situaciones abstractas como en contextos reales.
Lo anterior es la antesala para el desarrollo de habilidades durante la secundaria, entre ellas: identificar, interpretar y comprender fenómenos visuales y físicos del entorno que impliquen movimiento y medición.
Es importante señalar que durante todos los años de formación, tanto en primaria como durante la secundaria, se deben emplear representaciones de diversos tipos de acuerdo con el año escolar: lenguaje cotidiano, formal, simbólico o técnico, de manera escrita, visual u oral incluyendo imágenes, coordenadas rectangulares o software de Geometría dinámica (MEP, 2012; OCDE, 2017).
La pregunta que surge es ¿cómo favorecer el pensamiento geométrico en las aulas de primaria?, a continuación tres ideas:
Idea 1. Diversidad de formas y posiciones
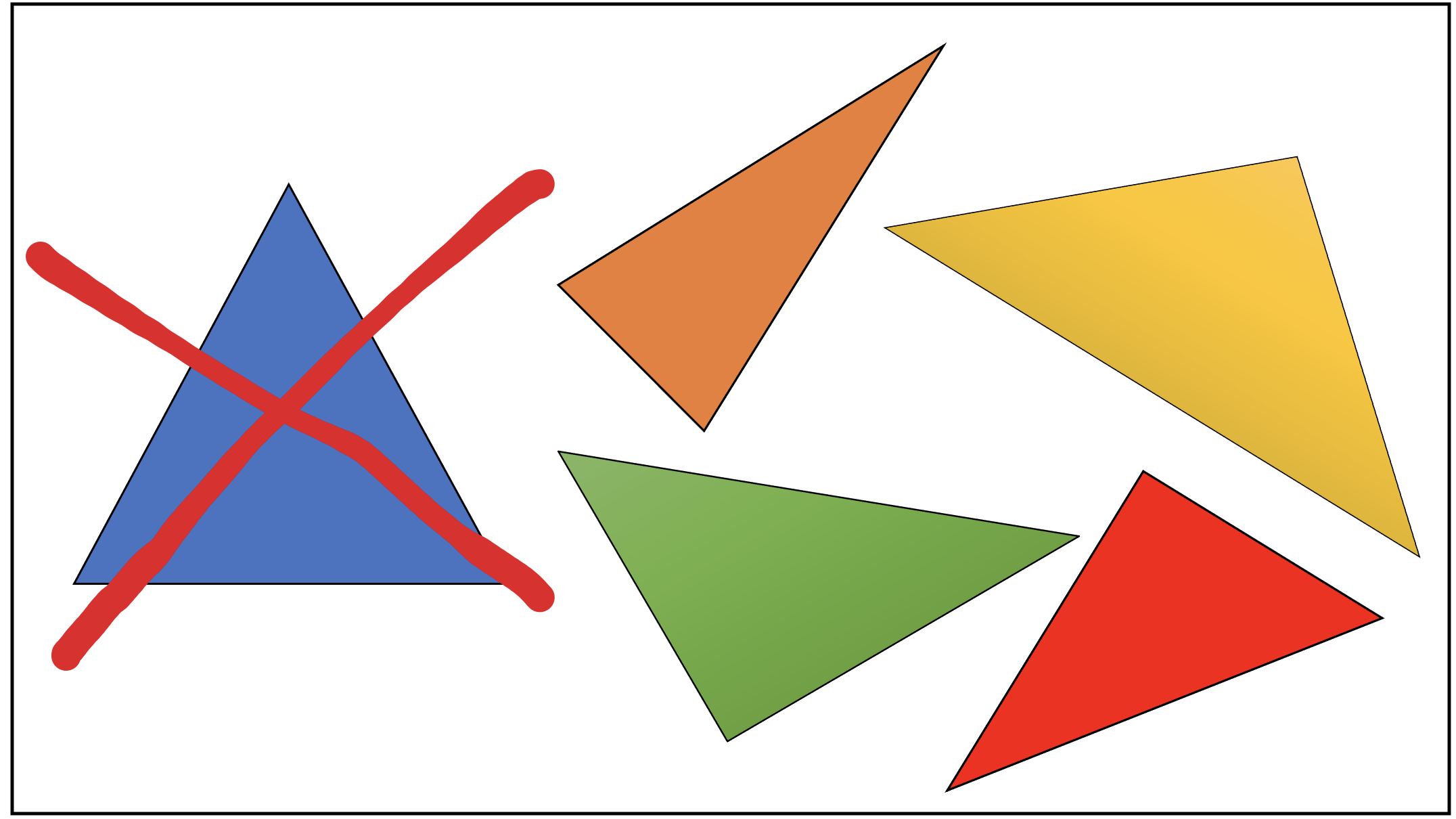
Las figuras prototipo son un obstáculo para realizar procesos de identificación básicos (Bernabeu y Llinares, 2017). Por ejemplo, si en la clase de Matemáticas cada vez que se trabajar el triángulo, la representación gráfica usada es un triángulo equilátero con la base ubicada de manera paralela a la horizontal, este objeto matemático perderá su diversidad y se transmitirá la idea errónea que la figura es estática. Se debe recordar que también existen triángulos isósceles y escalenos, y ellos a su vez pueden ser rectángulos, acutángulos y obtusángulos y se pueden ubicar de muchas maneras entonces ¿por qué emplear únicamente el triángulo equilátero y una posición estándar?
Consejo: Utilizar diversas representaciones de los objetos geométricos de manera que no existan prototipos. Se debe transmitir la idea de diversidad y movimiento.
Idea 2. Diversas representaciones
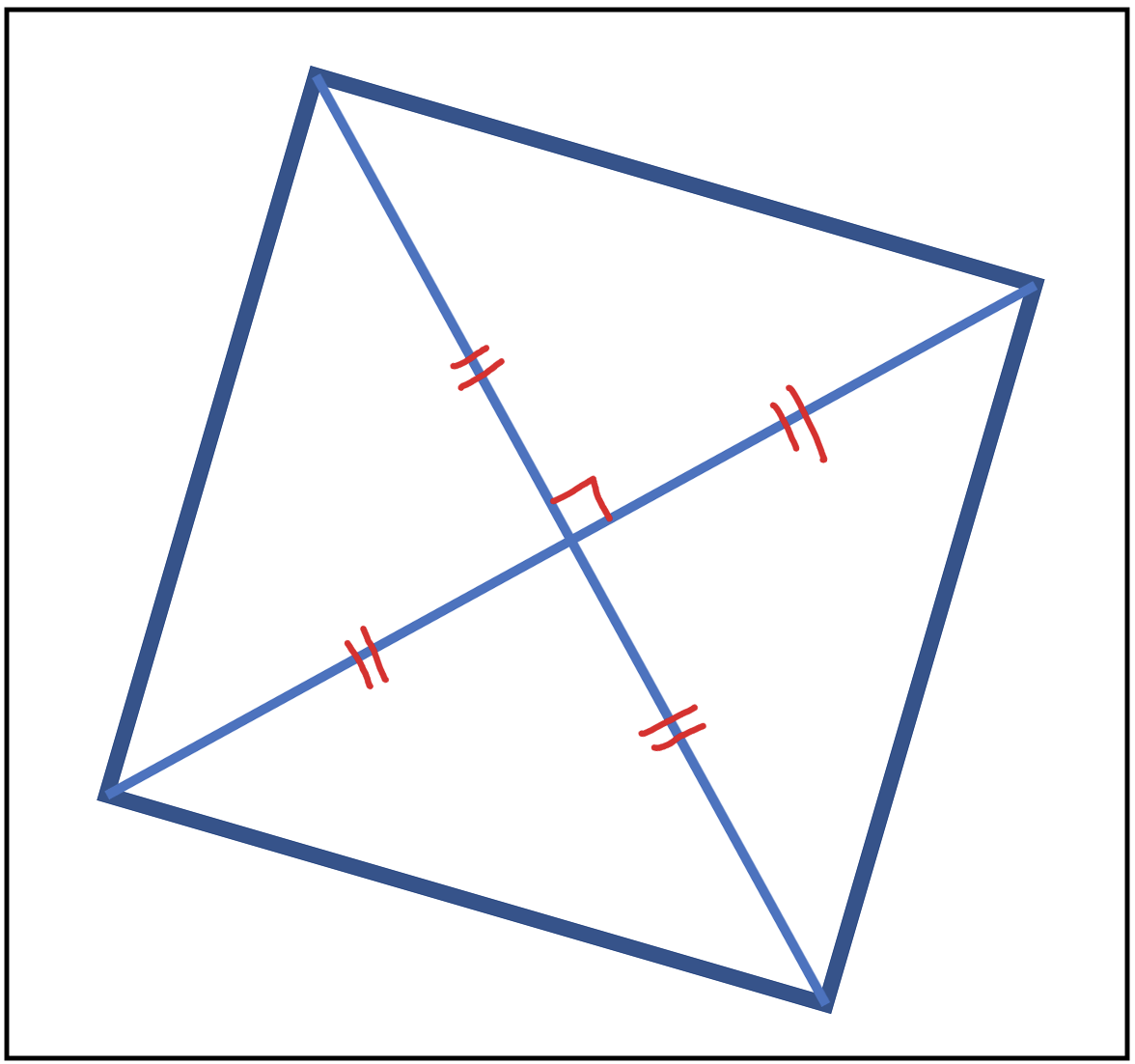
Proponer retos que impliquen usar, probar o descubrir propiedades de los objetos geométricos, un ejemplo es la siguiente actividad ¿Cómo se clasifican los triángulos que se generan al trazar las diagonales de un cuadrado? Justifique su respuesta, esta tarea matemática implica que la persona estudiante pase de la representación literal a una representación gráfica, ya sea en el papel, en algún dispositivo o en su imaginación. Y de inmediato, que empleé algunos otros objetos geométricos como la “diagonal de un cuadrilátero”, en particular el cuadrado y sus propiedades; posteriormente, utilizará la clasificación de triángulos para justificar su respuesta, de manera que se favorece el proceso matemático razonar y argumentar (MEP, 2012).
Consejo: Usar tareas matemáticas que impliquen el uso de diversas representaciones y el uso de las propiedades de objetos geométricos para promover la reflexión sobre ellas favoreciendo su comprensión.
Idea 3. Usar el contexto
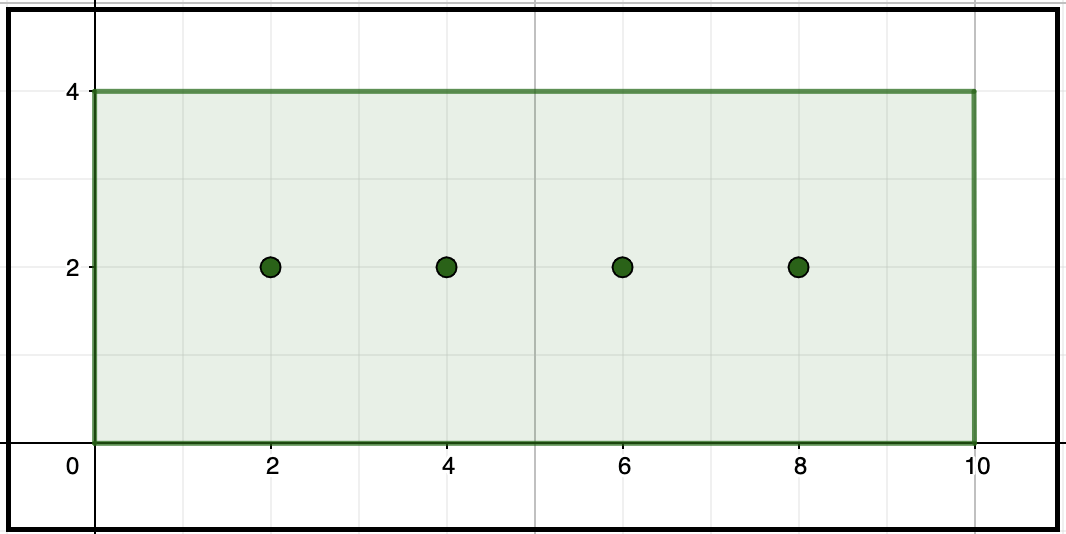
Un problema contextualizado por lo general implica emplear de manera simultánea varias habilidades, por tanto, es un recurso didáctico idóneo para recolectar evidencias de las destrezas del estudiantado. Por ejemplo se puede plantear un problema como el siguiente: Adela tiene una idea novedosa para su jardín, lo colocará en gradas, como se ve en la imagen.
La estructura posee las siguientes dimensiones: 1 m de largo por 40 cm de ancho y una altura de 60 cm máximo. Adela quiere cultivar un tipo de suculenta y quiere comprar el número exacto de plantitas considerando que le recomendaron trasplantarlas con una distancia de aproximadamente de 20 cm entre ellas y dejar 20 cm de los bordes ¿Cuántas plantas debe comprar Adela de acuerdo con las dimensiones de su jardín en gradas?
Para resolver el problema, la persona estudiante debe extraer del contexto planteado la información necesaria para dar respuesta a la pregunta, deberá identificar tres cosas para cálcular el número de plantitas: (1) la medida del largo en centímetros, (2) la medida del ancho y (3) las condiciones para trasplantar. Por tanto, ha empleado de la figura trimensional original solo lo que necesita y ha transformado información que se ofreció en lenguaje cotidiano a una representación matemática que modela la realidad, de manera que puede responder que Adela debe adquirir 12 plantitas.
Consejo: Emplear situaciones contextualizadas para promover de manera simultánea el uso de los objetos geométricos, sus propiedades y diversas representaciones.
Finalmente, espero que estas tres ideas sean de utilidad para el trabajo de aula y sí los consejos fueron de utilidad, por favor comparte esta entrada con otros colegas.
Referencias
Bernabeu, M. y Llinares, S. (2017). Comprensión de las figuras geométricas en niños de 6-9 años. Educación Matemática, 29(2), 9-35. DOI: 10.24844/EM2902.01
Ministerio de Educación Pública [MEP]. (2012). Programas de Estudio de Matemáticas. I, II y III Ciclos de la Educación General Básica y Ciclo Diversificado. San José, Costa Rica: autor.
Organización para la Cooperación y el Desarrollo Económico [OCDE]. (2017). Marco de Evaluación y de Análisis de PISA para el Desarrollo: Lectura, matemáticas y