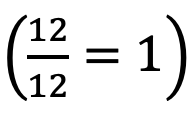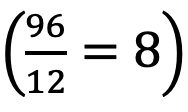Según la Organización para la Cooperación y el Desarrollo Económico (OCDE) el proceso de cuantificar implica comprender aspectos como: la medición, las magnitudes, las unidades, los indicadores, el tamaño relativo y los patrones, entre otros. El cálculo está implícito en la cuantificación y se realiza mentalmente o mediante algún dispositivo. Además, el valor hallado puede ser exacto, o de acuerdo con algún contexto bastará una aproximación (OCDE, 2017).
Las fracciones son parte importante de la cuantificación. Ellas, sus múltiples representaciones y su operatoria requieren práctica constante. Por esa razón aquí se presenta una operación que implica la multiplicación de fracciones y algunas ideas para fortalecer la cuantificación.
Multiplicación de Fracciones
Supongamos que se quiere hallar el producto de 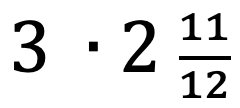
Esto es determinar a cuánto equivale 3 veces ![]()
Tenemos varias alternativas, aquí se mostrarán tres. Se debe recordar que la multiplicación es una suma reiterada y esto genera una de las soluciones propuestas.
También podemos transformar la fracción impropia a un número mixto:
A continuación, se han señalado algunas secciones de manera que sea más fácil de referenciar.
- Idea importante en la estrategia de solución A
Se suman las unidades y se agrupan las fracciones. Además, se suman las fracciones de manera conveniente, agrupando aquellas que forman unidades (ver número 1):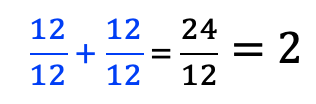
- Idea importante en la estrategia de solución B
La multiplicación se puede separar. Se multiplica 3 por el número entero y 3 por la fracción propia, como se señala con el número 2.
- Idea importante en la estrategia de solución C
Se debe recordar que la notación mixta de una fracción impropia significa “unidades más una fracción propia”, como se señala con el número 3.
Reflexiones finales
– Las soluciones se deben adaptar al nivel educativo y también a los propósitos de aprendizaje.
– El uso de la fracción que representa la unidad es fundamental
-Así como hallar unidades en una representación fraccionaria
-El manejo del número mixto en la multiplicación y la suma de fracciones es flexible, como se ha mostrado aquí. Esa flexibilidad favorece el cálculo mental y la estimación.
Existen algunos otros aspectos muy interesantes de la multiplicación que se pueden explorar a través de la representación gráfica de este caso, pero ese tema se abordará próximamente en otra entrada. Le invito a estar pendiente de la próxima publicación.
Referencia
Organización para la Cooperación y el Desarrollo Económico [OCDE]. (2017). Marco de Evaluación y de Análisis de PISA para el Desarrollo: Lectura, matemáticas y ciencias, Versión preliminar, Paris: OECD Publishing. Recuperado de https://www.oecd.org/pisa/aboutpisa/ebook%20-%20PISA-D%20FrameworkPRELIMINARY%20versionSPANISH.pdf