Desde que los estudiantes se encuentran en preescolar o los primeros años de la educación primaria, busca representar los números, letras, palabras, figuras de acuerdo con un sistema de símbolos que en muchas ocasiones dista de la simbología usada convencionalmente. (Brizuela, Blanton, Gardiner, Newman-Owens y Sawrey, 2015; Brizuela, Blanton, Sawrey, Newman-Owens y Gardiner, 2015; Ferreiro y Teberosky, 1979; Küchemann, 1981). Por lo anterior, es natural que los estudiantes utilicen diferentes representaciones para un concepto nuevo de matemática, en nuestro caso, las funciones.
Para desarrollar el pensamiento funcional es fundamental el conocimiento y análisis de los diferentes sistemas de representación de una función matemática. (NCTM, 2003). Algunos de estos sistemas de representación son:
Pictórico:
Este tipo de representación utiliza algún tipo de dibujo o grafo para representar la relación entre los datos.
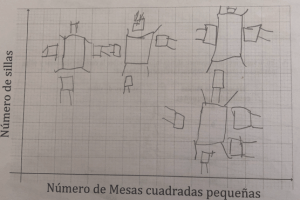
Figura 1: Representación pictórica de un problema de mesas y sillas
Tabular:
Posee un formato rectangular compuesto de encabezados y cuerpo de datos, localizados en filas y columnas. Las tablas difieren en variedad, estructura, flexibilidad, notación, representación y uso. (Estrella, 2014).
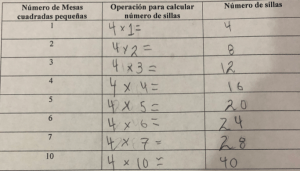
Figura 2: Representación tabular de un problema de mesas y sillas
Natural (Escrito o verbal):
Se utilizan palabras y frases de lenguaje cotidiano para expresar la relación, sin embargo, no es fácil visualizar la relación entre dos cantidades con esta representación.
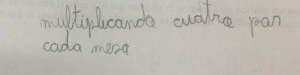
Figura 3: Representación natural de un problema de mesas y sillas
Simbólica:
Rico (2009), explica que una función puede representarse a través de números y letras que cumplen cierta sintaxis. Cuando se utilizan números (operaciones y resultados) se dice que es una representación simbólica numérica mientras que la simbólica algebraica es cuando se utilizan números, letras y operaciones para expresar la generalización. Para Merino, Cañadas y Molina (2013), el uso de simbolismo algebraico supone un mayor grado de abstracción.

Figura 4: Representación simbólica de un problema de mesas y sillas
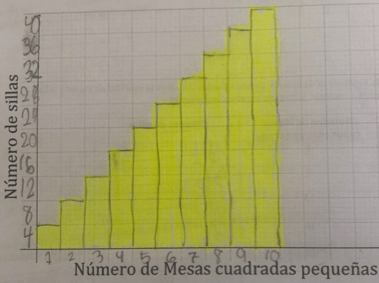
Gráfica:
Se utiliza algún sistema de coordenadas para representar la relación entre las variables a través de puntos cuyas coordenadas son de la forma (x,y). Para algunos autores (Brenner et al, 1997), al resolver un problema y utilizar una representación como la gráfica, no es necesario el cumplimiento estricto de las convenciones para realizar los gráficos. Para estos autores para que una gráfica pueda ser considerada como tal, es necesario que se representen los ejes con intervalos escalonados y que se visualice la representación lineal presente en el problema de alguna manera.
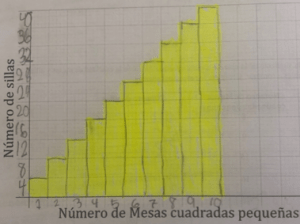
Figura 5: Representación gráfica de un problema de mesas y sillas
Múltiples:
Una representación múltiple es aquella donde se utilizan dos o mas representaciones anteriores. Por otro lado, Cañadas y Figueiras (2010) distinguen dos tipos de representación múltiple: (a) combinadas que son aquellas representaciones que resultan de una combinación de dos o más de los sistemas de representación citados anteriormente; y (b) sintéticas, cuando se utilizan dos o más representaciones pero que ninguna por sí misma da sentido a la resolución.
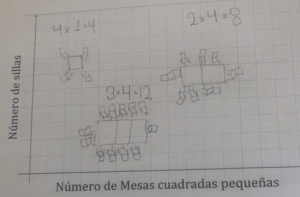
Figura 6: Representación múltiple de un problema de mesas y sillas
Referencias:
Brenner et al (1997). Learning by understanding: The Role of Multiple Representations in Learning Algebra. American Educational Research Journal. Vol 34, No 4, 663-689.
Brizuela, B., Blanton, M., Gardiner, A., Newman-Owens, A. y Sawrey, K. (2015). A first grade student’s exploration of variable and variable notation. Estudios de Psicología, 36, 138–165.
Brizuela, B., Blanton, M., Sawrey, K., Newman-Owens, A. M. y Gardiner, A. (2015). Children’s use of variables and variable notation to represent their algebraic ideas. Mathematical Thinking and Learning, 17, 1-30.
Cañadas, M.C. y Figueiras, L. (2010). Razonamiento y estrategias en la transición a la generalización en un problema de combinatoria. PNA, 4(2), 73-86.
Estrella, S. (2014). El formato tabular: una revisión de literatura. Revista Electrónica Actualidades Investigativas en Educación, 14(2).
Ferreiro, E., & Teberosky, A. (1979). Los sistemas de escritura en el desarrollo del niño [Literacy before schooling]. Buenos Aires: Siglo Veintiuno Editores.
Küchemann, D. E. (1981). Algebra. In K. Hart (Ed.), Children’s understanding of mathematics (pp. 102–119). London: Murray.
Merino, E., Cañadas, M. C. y Molina, M. (2013). Uso de representaciones y patrones por alumnos de quinto de educación primaria en una tarea de generalización. Edma 0-6: Educación Matemática en la Infancia, 2(1), 24-40.
National Council of Teachers of Mathematics. (2003). Principios y estándares para la educación matemática [Traducción de Manuel Fernández Reyes]. Sevilla: Sociedad Andaluza para la Educación Matemática “THALES”.
Rico, L. (2009). Sobre las nociones de representación y comprensión en la investigación en educación matemática. PNA, 4(1), 1-14.
Académico de la Universidad Nacional de Costa Rica y del Ministerio de Educación Pública.