Una de las ideas motrices de los Programas de Matemáticas es la manera como define su enfoque principal. Este podría haber sido distinto, algo acerca del cultivo de capacidades superiores, o sobre la competencia general. No obstante, se condensó de una forma que permitiera visualizar fácilmente su naturaleza.
El enfoque principal se consigna como “Resolución de problemas, con énfasis en contextos reales”. Se trata de una estrategia pedagógica, no de un ajuste de contenidos. Su finalidad última es transformar la acción de aula.

Esta estrategia de aula es la forma precisa en que se busca implementar un currículo lleno de objetos teóricos nuevos y organizados con una perspectiva innovadora. Habría sido posible no plantearla, pero era necesaria para aterrizar la visión curricular, precisarla, y también para dotar a los agentes educativos de herramientas para sostener sus quehaceres.
Esta acepción de “Resolución de problemas” es aquí muy precisa. Se distancia de aquellas acepciones más generales, que refieren a la capacidad cognitiva. Precisamente en el currículo se usa la capacidad cognitiva “plantear y resolver problemas” y se condensa como un proceso. Y se quiso ser aún más precisos.
Un modelo de lección
La resolución de problemas como estrategia para la construcción de aprendizajes propone una acción de aula resumida en cuatro momentos: presentación del problema, trabajo independiente de los estudiantes, contrastación y comunicación de estrategias seguidas en la fase independiente, y cierre o clausura de la lección. En cada momento el docente debe realizar tareas específicas.
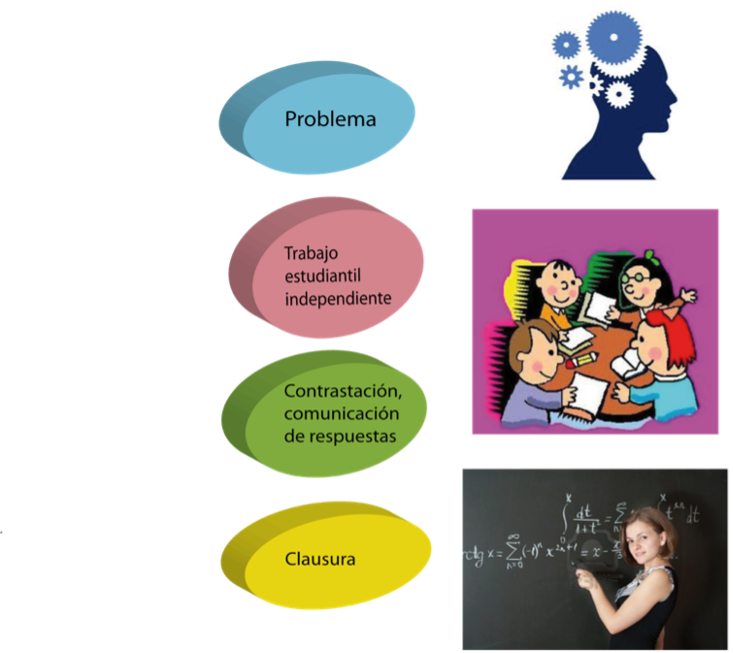
Como estrategia de acción de aula los cuatro momentos deberán complementarse con sesiones de movilización de los aprendizajes realizados, es decir de actividades que permitan la memorización y automatización de los conocimientos aprendidos (objetos y métodos) y su aplicación en diversas situaciones. Estos no deben estar lejos del enfoque creativo, estimulante y constructivo que debe predominar en las lecciones de construcción de aprendizajes.
Epistemológicamente, la propuesta afirma la necesidad de que el estudiante construya sus propios aprendizajes y busca fortalecer su compromiso con ellos. Para eso se plantea que la lección proporcione problemas interesantes que capturen la atención estudiantil y a la vez que sean desafíos para motivar su acción cognitiva.
Los contextos reales
El énfasis en contextos reales obedece tanto a ese propósito como al que parte de una consideración sobre la naturaleza de las Matemáticas: los objetos matemáticos refieren en su base a las relaciones de los sujetos con la realidad física y social, son modelos de lo real o modelos de modelos en sucesiones de mayor nivel de abstracción. Los contextos reales permiten una manipulación de los métodos generales de construcción matemática.
Esta visión de la resolución de problemas se apodera de los enunciados constructivistas y además les da sentido práctico pedagógico. Pero va más lejos: el o la docente debe también intervenir adecuadamente en el proceso y debe en su momento ser el transmisor (o puente) del conocimiento y de la cultura matemática de la época (adaptados a entornos escolares, su “transposición didáctica”).
El nuevo currículo asume la formación matemática escolar orientada a la construcción de capacidades de la ciudadanía en el uso de las Matemáticas para su vida, ya sean sus contenidos o como destrezas intelectuales generadas con el aprendizaje de la asignatura. La naturaleza de las Matemáticas que se adopta enfatiza su carácter sociohistórico, cultural y su asociación con la realidad física y social. La Educación Matemática se asume como una práctica y su investigación como una ciencia social independiente de las Matemáticas y de la pedagogía general.
En el currículo: “(…) la competencia matemática se formula en relación con el uso de las Matemáticas para describir, comprender y actuar en diversos contextos de su realidad (personales, físicos, sociales, culturales).”
Por todo eso, el énfasis de esta resolución de problemas (estrategia pedagógica) son los contextos reales, aunque también los contextos matemáticos se valoran por su papel crucial.
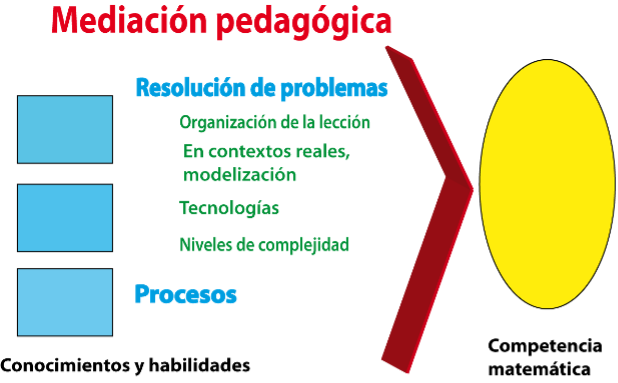
Al visualizarse la preparación escolar de esta manera, el currículo necesitó incluir sus objetos y enfoques de manera coherente con ese propósito. Eso influenció, por ejemplo, el papel de áreas matemáticas, la selección y significado de contenidos. Lo veremos luego.
El enfoque principal que invoca resolución de problemas y énfasis en contextos reales ya muestra una perspectiva distinta en relación con currículos anteriores. Los conceptos de habilidades, procesos, niveles de complejidad y competencia se mueven sobre ese territorio intelectual.

Ángel Ruiz es especialista en la Historia y Filosofía de las Matemáticas, y en diversos temas de la Educación Matemática, especialmente el currículo.
Tiene más de 300 publicaciones académicas (incluidos 36 libros).
Ha sido conferencista invitado en más de 170 eventos presenciales en 25 países de todos los continentes.
Es el único latinoamericano que ha ocupado durante dos mandatos la vicepresidencia de la Comisión Internacional de Instrucción Matemática ICMI.
Fue durante 8 años miembro de la Comisión de Países en Desarrollo de la Unión Matemática Internacional.
Ángel ha sido presidente del Comité Interamericano de Educación Matemática desde 2007.
Desde 2012 ha sido director/presidente de la Red de Educación Matemática de América Central y El Caribe.




















