La competencia general y capacidades transversales (o procesos) son las capacidades generales del currículo costarricense. Estas se plantean promover a través o a partir del trabajo preciso con las habilidades específicas y generales sobre los conocimientos matemáticos seleccionados. ¿Cómo? En la mediación pedagógica. Esta mediación incluye la resolución de problemas como estrategia pedagógica central, pero también el énfasis en contextos reales, el uso de problemas en varios niveles de complejidad que activen procesos. Desarrollar habilidades y capacidades transversales debe hacerse a la vez.
Procesos y capacidades superiores transversales
Los procesos se deben generar en las cinco áreas matemáticas que seleccionó el currículo: Medidas, Números, Geometría, Relaciones y álgebra y Estadística y probabilidad.
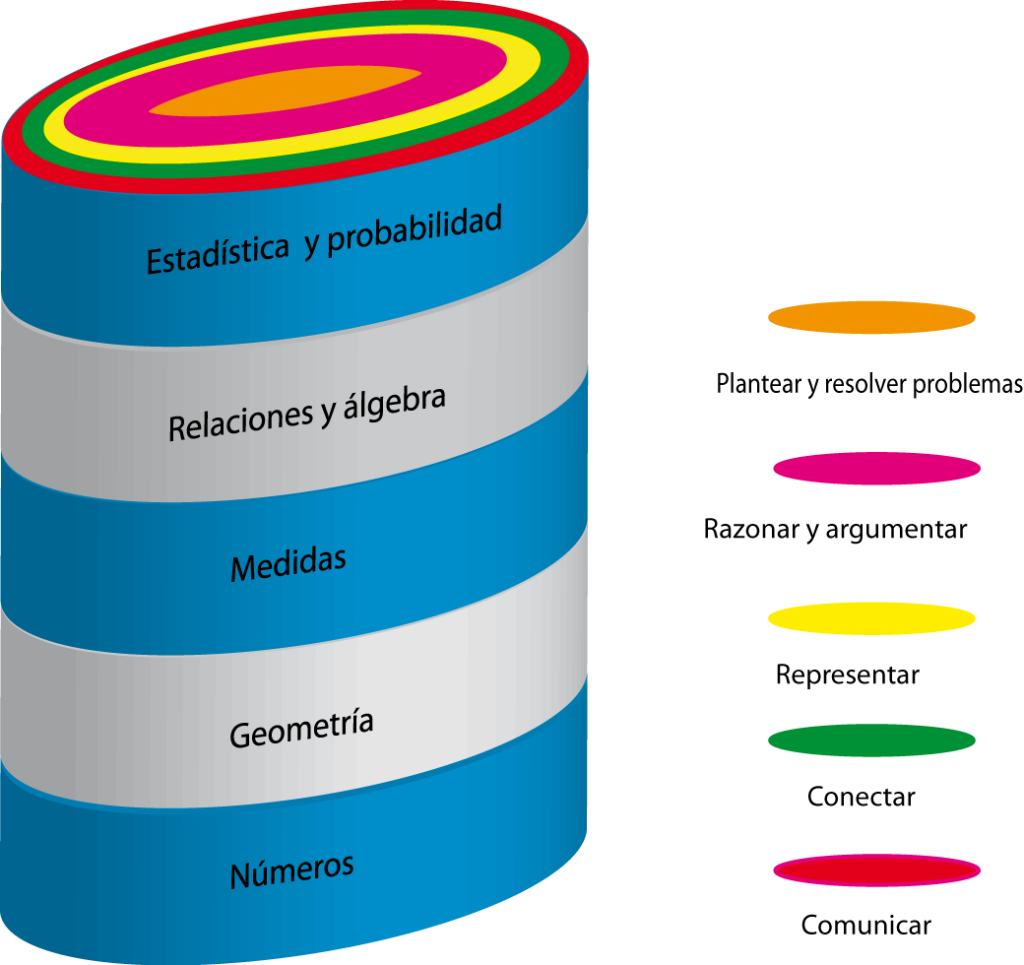
Los “procesos matemáticos” del currículo son cinco.
Razonar y argumentar
El proceso se activa en todas las áreas de múltiples maneras, por ejemplo en el estudio de regularidades y patrones, en la justificación de la congruencia de triángulos, la elección de una representación matemática y su manipulación, en la solución de ecuaciones, entre otros. La justificación y prueba son parte esencial de los quehaceres matemáticos y por lo tanto deben ocupar un lugar especial en la formación escolar.
Plantear y resolver problemas
Hay algunos elementos que vale la pena subrayar. En primer lugar, que no todo problema permite conducir a ideas matemáticas aunque sea interesante o divertido, por eso la acción docente es decisiva para el diseño de problemas apropiados. En segundo lugar, en cada área matemática es posible realizar este proceso de distintas maneras, pero siempre gradualmente. Las estrategias para la resolución de problemas deben ser introducidas no de forma abstracta sino en las instancias específicas en los problemas escogidos: a veces será potenciar el uso de diagramas, otras el reconocimiento de patrones, o la prueba con la exhibición de casos, etc. Igualmente, es necesario entrenar a los estudiantes en las diferentes etapas de la resolución de problemas como la comprensión de los mismos, el trazado de planes de acción y la evaluación o monitoreo de las acciones.
Comunicar
Este proceso está asociado a una característica esencial de los quehaceres matemáticos: una idea matemática para ser “correcta” debe ser aceptada por una comunidad profesional de matemáticos. Existen reglas específicas para hacer esto, lo cual es importante de incluir en los programas es colares. El proceso sugiere la comunicación en distintos niveles y formas, desde las más simples como verbales o escritas, hasta gráficas, simbólicas y formales.
Conectar
Es necesario tener una visión amplia de lo que este proceso supone en el medio educativo. Las conexiones se pueden desarrollar en muchos contextos: por ejemplo, dentro de cada área matemática (como cuando se aplican los procedimientos y operaciones de los números naturales en los racionales o reales). Pero también entre las distintas áreas matemáticas y de manera general con otras materias. Las Matemáticas, por su misma naturaleza, poseen las potencialidades para apoyar los procesos transdisciplinarios que desde los primeros años escolares se deben cultivar. El conocimiento debe visualizarse como una realidad interconectada llena de enlaces.
Representar
Pretende fomentar el reconocimiento, interpretación y manipulación de representaciones múltiples que poseen las nociones matemáticas (gráficas, numéricas, visuales, simbólicas, tabulares). el proceso busca favorecer la capacidad para elaborar y usar representaciones matemáticas que sirvan en el registro y organización de objetos matemáticos, para interpretar y modelar situaciones propiamente matemáticas, para manipular distintas representaciones de objetos matemáticos. Propone también desarrollar capacidades para poder traducir una representación en términos de otras, comprendiendo las ventajas o desventajas (o los alcances) de cada representación en una situación determinada.
Los procesos seleccionados trabajan de manera integrada y provocan gradualmente capacidades transversales, fortaleciendo a la vez la generación de las habilidades. Es un proceso integrado, sinérgico, holístico.
Se puede identificar “procesos” con “capacidades cognitivas superiores transversales”. Los primeros, en rigor, son acciones que generan las segundas. Se definieron así para subrayar el carácter activo del desarrollo de capacidades superiores. Pero no hay error si en una acción educativa se usan como términos equivalentes.

Niveles de complejidad
Otro medio en el aula para provocar el desarrollo de las capacidades cognitivas superiores y la competencia general es el trabajo de los problemas en diversos niveles de complejidad.
Es necesario aclarar de primera entrada la distinción entre problema y ejercicio: en el primero se requiere la participación de acciones cognitivas nuevas para el sujeto. Lo que puede ser un problema para un estudiante, para otro puede no serlo. El currículo asume por conveniencia los tres niveles de complejidad: reproducción, conexión y reflexión, esencialmente como fueron conceptualizados por PISA en el año 2003.
Coherencia de instrumentos con el currículo
El planeamiento, gestión y desarrollo de aula y la evaluación deben tomar en cuenta los conocimientos, habilidades, procesos matemáticos y distintos niveles de complejidad.
Desafortunadamente, varios de los instrumentos educativos ofrecidos por las autoridades educativas no incluyen todos estos elementos de la forma apropiada, y especialmente hay debilidades en cuanto a procesos y niveles de complejidad. Por ejemplo, esto ha sucedido en las diversas pruebas nacionales desde Bachillerato, FARO hasta las recientes estandarizadas nacionales del 2023. Es muy difícil que estudiantes y docentes implementen procesos, niveles de complejidad o por el otro lado integración de habilidades en sus quehaceres si los instrumentos educativos nacionales no lo hacen.
No incluir procesos y niveles de complejidad resultaría más sencillo. Pero se traiciona un propósito medular de este currículo.
Comprender la forma en que se articulan todos los elementos curriculares aquí mencionados es fundamental. Se parte de lecciones de la educación matemática en el mundo, pero es producto de una construcción intelectual realizada con una perspectiva costarricense y utiliza ideas que fueron planteadas en este país desde los años 1990s. Es un planteamiento original.

Ángel Ruiz es especialista en la Historia y Filosofía de las Matemáticas, y en diversos temas de la Educación Matemática, especialmente el currículo.
Tiene más de 300 publicaciones académicas (incluidos 36 libros).
Ha sido conferencista invitado en más de 170 eventos presenciales en 25 países de todos los continentes.
Es el único latinoamericano que ha ocupado durante dos mandatos la vicepresidencia de la Comisión Internacional de Instrucción Matemática ICMI.
Fue durante 8 años miembro de la Comisión de Países en Desarrollo de la Unión Matemática Internacional.
Ángel ha sido presidente del Comité Interamericano de Educación Matemática desde 2007.
Desde 2012 ha sido director/presidente de la Red de Educación Matemática de América Central y El Caribe.




















