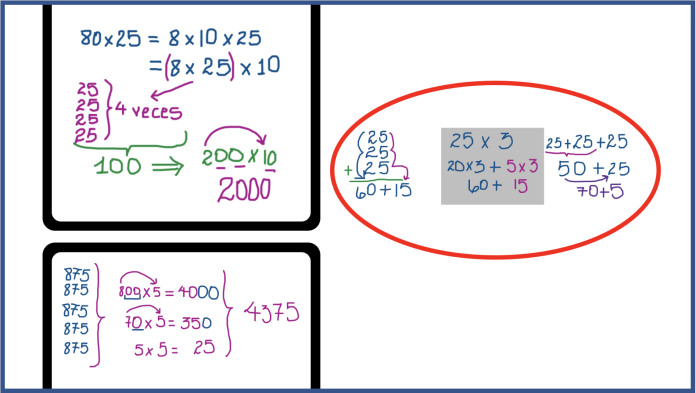Marianela Zumbado-Castro, UNED
Ricardo Poveda-Vásquez, UNA
Desde hace muchos años, los resultados de los congresos internacionales de educación matemática y las propuestas de los investigadores de esta disciplina han incentivado a incorporar el sentido numérico en los currículos de cada país. Entonces, surgen interrogantes como ¿qué es sentido numérico?, ¿por qué se incorporó en los Programas de estudio de Matemática de Costa Rica en 2012?, y ¿cómo se hizo?, aquí encontrará algunas ideas que dan respuesta a estas interrogantes y algunos elementos más.
¿Qué es el sentido numérico?
Es un conjunto de destrezas que se desarrollan al margen de la memorización de las propiedades y las operaciones de los conjuntos numéricos. El énfasis está en el manejo práctico de los números en contextos reales, dando relevancia a los cálculos (cómputos), por tanto, implica fortalecer el cálculo mental, la estimación y la razonabilidad de la selección de las operaciones por realizar en situaciones determinadas. Además, el sentido numérico, según se describe en los Estándares de Educación de la National Council of Teachers of Mathematics (NCTM) es:
(…) la habilidad para descomponer números de forma natural, utilizar ciertos números como 100 o 1/2 como referentes, usar las relaciones entre las operaciones aritméticas para resolver problemas, comprender el sistema decimal de numeración, estimar, dar sentido a los números y reconocer las magnitudes relativa y absoluta de los números (NCTM, 2000, p. 34)
¿Por qué se incorpora en los Programas de estudio de Matemática de Costa Rica en 2012?, y ¿Cómo se hace?
Las investigaciones internacionales demuestran la importancia del sentido numérico. Las personas requieren realizar cálculos y aproximaciones de manera rápida y correcta. Así como, poseer la capacidad de decidir la estrategia pertinente de solución. Por esta razón, se incluye en los ciclos de la Educación General Básica de manera que en los dos primeros es su foco principal, en el tercero posee una presencia notable. En Educación Diversificada su presencia es transversal, aunque el área de Números no está en los últimos años escolares siempre se promueven tareas matemáticas que implican la aproximación.
Algunos aspectos fundamentales para desarrollar este sentido son: (1) la descomposición de los números para facilitar los cálculos, (2) la representación múltiple del número, como por ejemplo en el caso de las fracciones, que se pueden denotar en su forma fraccionaria, decimal, gráfica, entre otras, (3) la experimentación y dominio de las propiedades de los números: pares, impares, primos, compuestos, cuadrados, entre otros, (4) establecer el vínculo entre las operaciones básicas, (5) estimar y juzgar que los resultados obtenidos al desarrollar operaciones y resolver problemas, sean razonables (Ministerio de Educación Pública, 2012).
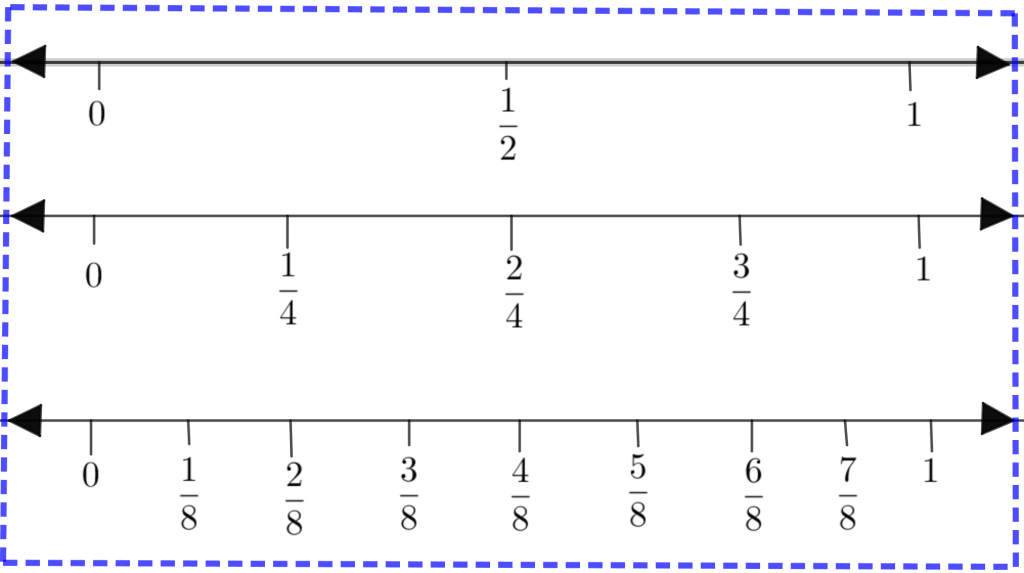
En los programas de matemáticas del MEP, el área de números en el I Ciclo busca “desarrollar el concepto de número para poder utilizarlo en diferentes situaciones, comprender los significados de las operaciones básicas” (MEP, 2012, p. 83). En este ciclo el énfasis son los números naturales, mientras que en el II Ciclo la prioridad son las fracciones, sus representaciones y la operacionalización de las mismas.
En el III Ciclo se trabajan los números naturales, los enteros, los racionales, los irracionales y los reales, no desde una perspectiva conjuntista, sino el concepto de estos números y la resolución de operaciones.
Habilidades para la vida
En los programas oficiales del MEP (2012) se declara que es para ellos la competencia matemática y se adopta la siguiente descripción:
(…) una capacidad del individuo para formular, emplear e interpretar las Matemáticas en una variedad de contextos. Incluye razonar matemáticamente y usar conceptos, procedimientos, hechos y herramientas para describir, explicar y predecir fenómenos. Ayuda a los individuos a reconocer el papel de las Matemáticas en el mundo y hacer juicios bien fundados y decisiones necesarias para ciudadanos constructivos, comprometidos y reflexivos (OECD, 2010, p. 4) (MEP, 2012 p. 23).
La relación sentido numérico y competencia matemática es estrecha debido a que el razonamiento matemático se ve favorecido cuando el manejo práctico de los números, sus cómputos y la selección de la estrategia más efectiva se realizan de forma rápida y acertada en relación con el entorno.
Respecto a la selección de la estrategia, por ejemplo, cuando se necesita realizar cálculos incómodos y extensos, la persona docente debe promover el uso de la calculadora por ser más conveniente, mientras que cuando se pretenden desarrollar las estrategias algorítmicas este recurso es innecesario.
Reflexiones finales
El sentido numérico debe ser promovido desde la perspectiva que se plantea en los programas del MEP(2012) con el propósito de garantizar ciudadanos capaces de ver la realidad y matematizar algunos de sus aspectos de manera rápida y efectiva. El inicio en etapas tempranas del desarrollo (I Ciclo) es fundamental, de manera que el estudiantado logre incluir en sus actividades diarias el cálculo mental y la estimación.
Referencias
Ministerio de Educación Pública. (2012). Programas de Estudio de Matemáticas. I, II y III Ciclos de la Educación General Básica y Ciclo Diversificado. San José: autor.
National Council of Teachers of Mathematics. (2000). Principles and standars for school mathematics. Reston, VA: autor
Académico de la Universidad Nacional de Costa Rica y del Ministerio de Educación Pública.